Measure Theory - Part 8 - Monotone convergence theorem (Proof and application)

This is the English version of the German video series.
Support the channel on Steady:

Official supporters in this month:
- William Ripley
- Petar Djurkovic
- Dov Bulka
- Lukas Mührke

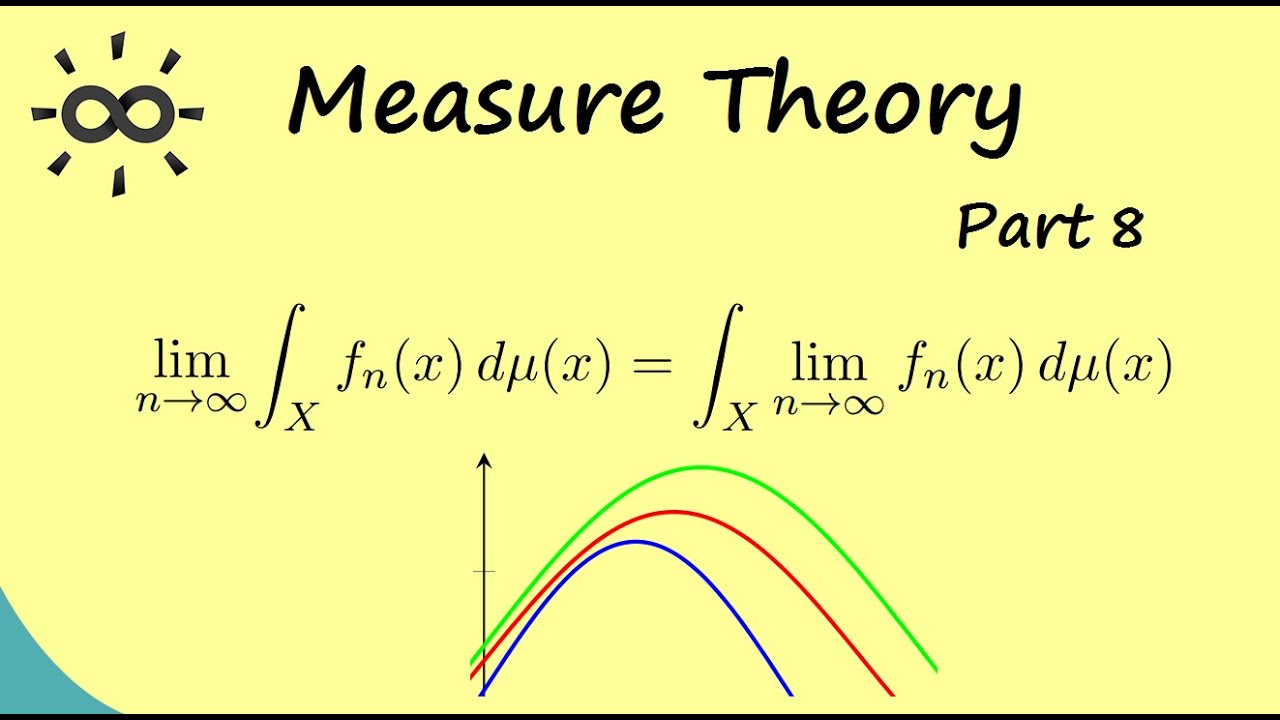
Here, I explain one of the interesting and important theorem of integral theory: The monotone convergence theorem, also known as "Beppo-Levi". Before showing the theorem, we go over some important properties of the integral.

I hope that this helps students, pupils and others.

(This explanation fits to lectures for students in their first year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

Mathematics (Field Of Study),Metric Space,metrischer Raum,Mathematik,Normed Space,normierter Raum,Analysis,Linear Algebra,lineare Algebra,1. Semester,Anschaulich,Definition,Student,Studium,Klausur,Aufgabe,Integral,Lebesgue,Riemann,Measure,Maß,Integrationstheorie,Maßtheorie,set,function,area,measure,integral,integration,learning,solution,Borel,help,derivative,dirac,Measure problem,axiom of choice,Lebesgue integral,Beppo Levi,monotonic,convergence,